Trace Calculation

Each pair of consecutive survey points can be joined using a great circle on the surface of a sphere, with the tangent to the circle at each survey point being the vector formed by the azimuth and dip at the point.

Using the shortest arc of these circles in each case, this series of circular arcs forms the drillhole trace. We approximate each circular arc with a series of line segments, making sure the distance between the line segments and the curve never exceeds 0.05 metres.

The Details

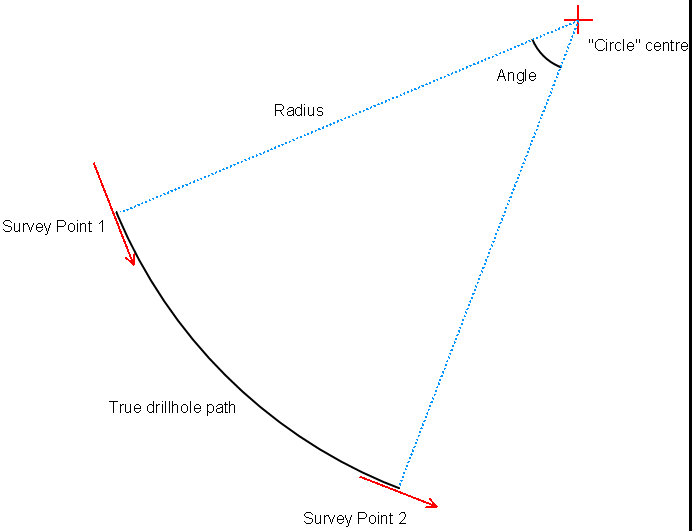
Take two consecutive survey points, with the position of the first point known (either it is the collar position, or the previous segment's calculated end point). From the azimuth and dip construct two unit vectors representing the direction at each survey point, and then calculate the angle between the two direction vectors using the dot product.

On a circle, the angle between two tangent vectors at two points is the same as the angle between the two points, so we now have the angle between the two survey points (as points on the circle segment between then). The radius of a circle can be found by dividing the length of an arc between two points on the circle by the angle between the two points. We have the angle, and the length is the difference in depth between the two survey points, so we can calculate the radius of the circle.

We can construct a unit vector representing the radius using the cross product of the two direction vectors:

tempVector = directionVector1 x directionVector2

radiusVector = directionVector1 x tempVector

We can then use the known position of the first point, the unit radius vector, and the radius to find the centre of the circle:

centrePoint = startPoint - radius * radiusVector

If the radius is greater than twice the maximum deviation we want (currently 0.05m), then we may need to create a series of line segments between the two survey points to approximate the curve. Then, if the angle between the two survey points is greater than

angleStepSize =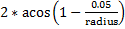

then the number of line segments we need to create is:

numberOfSteps = (angle / angleStepSize)

We can now use these calculated values to create the line segment end points by using vector rotations. For each point:

newRadiusVector = rotation of radiusVector around tempVector by angleStepSize * point number

segmentPoint = centrePoint + radius * newRadiusVector

And thus all the segment points are calculated.