Dependencies

On the Home tab, in the Setup group: Select Dependencies to setup dependencies between the tasks of the schedule.

In the Equipment Source Path, topic, we looked at how to build a Source Path. An advanced extension of Source Paths is the use of Dependencies, which is a logical application of "Don't do this until you've done this". A Dependency pairs Predecessors (do this before) and Successors (do this after).

There are different types of Dependencies, listed below in order of general performance impact (fastest to slowest):

  • Process Order

    • A Process Order Dependency is used to set dependencies between different processes, for example Blasting waits on Drilling. Any model with more than one Process should normally have a Process Order Dependency. Add multiple entries to set up the hierarchy and use Ranges if it changes in different regions.

  • Sequence

    • A Sequence Dependency is typically used to create top-down or bottom-up vertical dependencies between different Tasks within a group. Grouping Expression, Level Direction and Index parameters control how the lists of Tasks are created and in what order.

    The most commonly required change is the Level Direction of your Bench if your Bench doesn't follow a logical progress of first to last in the Index (e.g. if the first Indexed Bench in a Source Table is at the bottom instead of the top you would reverse the Level Direction).

  • Offset

    • An Offset Dependency is used to set regular dependencies between Tasks based on one or more Offsets. Commonly used for staggers where there are roughly regular sized Solids/Mining areas.

  • Range

    • A Range Dependency is used to set dependencies between ranges of tasks by explicitly defining Predecessor and Successor pairs. Range dependencies are commonly used to group blocks together to form a single shot together, limit mining in an area until access is established, ensure cast and dozer material isn't blasted until the coal in the previous strip is mined or in situations where anomalies need to be controlled.

  • Cone

    • Cone Dependencies create Dependencies based on the Direction and Angle between Process Centroids. Z Limit and Radius constrain the resulting Cone for performance. A rough guide for the fastest application of this (no excess Dependencies created) is that the radius should be a little larger than your Block or Strip width and the Z level should be about Radius/tan(Angle). If unsure you can always make the numbers a little larger.

  • Solid Overlap

    • A Solid Overlap Dependency compares Solids in Plan View looking up, down or both directions based on a certain Overlap Percentage. The lower the Overlap Percentage the more likely a Dependency will be created. The Expand Option will look further around the Solid and Grouping Expressions are used to improve performance by limiting the number of comparisons required.

As you can see each Dependency type has a "common" use but they can be flexible depending on your requirements and understanding of how they work. To fully understand Dependencies, additional concepts are detailed in: Dependencies: When and Where?.

Released vs Unreleased

The key terminology to be aware of is Released (no Dependency on this Task) and Unreleased (Waiting on Dependency). This will become useful in the Snapshot Viewer and how it can help diagnose issues with Source Paths and Dependencies.

Pairing (Range Dependencies)

The most important concept before creating your first Range Dependency is to know how Wildcards and Spans are applied. Let's start with something simple, say you wanted to make sure that in Strip 1, Blocks 1-10, Seam G didn't start until Seams A-F were fully completed. You might write your dependency like this:

Predecessor: MyPit/S1/B1-B10/A-F
Successor: MyPit/S1/B1-B10/G

When you write a Span in a dependency (or a Wildcard) what you are doing is grouping the entire set of Predecessor Nodes (MyPit/S1/B1-B10/A-F) and then pairing that group with the Successor Nodes (MyPit/S1/B1-B10/G).

Key Concept: No Leaf inside the Successor pair can be worked until every Leaf inside in the Predecessor pair is 100% worked.

So in the example above, MyPit/S1/B6/G won't get worked until every Leaf in MyPit/S1/B1-B10/A-F had been worked. Instead of a single seam (G wait on A-F) Dependency let's say you want to make each seam (A,B,C etc) dependant on the seam before it being complete. You might be tempted to write your Dependency like this.

Predecessor: MyPit/S1/B1-B10/A-F
Successor: MyPit/S1/B1-B10/B-G INCORRECT

Just like in the example before it, everything in the Predecessor group must be finished before the Successor can be worked. In this example however there is an overlap between the groups which means that MyPit/S1/B1-B10/C is waiting on MyPit/S1/B1-B10/B (intended) but the opposite is also true (MyPit/S1/B1-B10/B is waiting on MyPit/S1/B1-B10/C) which will bring everything to a grinding halt.

What you actually want to do is explicitly pair each seam (A with B, B with C etc) and the way you do that is with Arrays.

Arrays (Range Dependencies)

However, in many/most examples you're going to want that explicit Node to Node pairing, so in order to pair only Predecessor Seam A with Successor Seam B etc. You could get this behaviour by writing individual dependencies per line like in the following example:

Predecessor: MyPit/S1/B1-B10/A Successor: MyPit/S1/B1-B10/B
Predecessor: MyPit/S1/B1-B10/B Successor: MyPit/S1/B1-B10/C
Predecessor: MyPit/S1/B1-B10/C Successor: MyPit/S1/B1-B10/D
Predecessor: MyPit/S1/B1-B10/D Successor: MyPit/S1/B1-B10/E etc

However you can usually address this more succinctly, for which you will need to use Arrays, which were addressed briefly in the Source Path documentation.

Predecessor: MyPit/S1/B1-B10/{A;B;C;D;E;F}
Successor: MyPit/S1/B1-B10/{B;C;D;E;F;G}

By writing your Dependency with an array, you are defining your pairs explicitly and therefore Seam A will pair with Seam B etc.

Multi-Dimensional Arrays (Range Dependencies)

In the example above, we've applied a Seam Dependency successfully using an array, but it groups all blocks 1-10 together.. If you want to specify this Dependency to work block by block, you need to introduce the concept of an additional dimension. It's a pretty simple addition to a regular array, except that you number each dimension of the array. It's a little easier to visualise than explain so look at the image below.

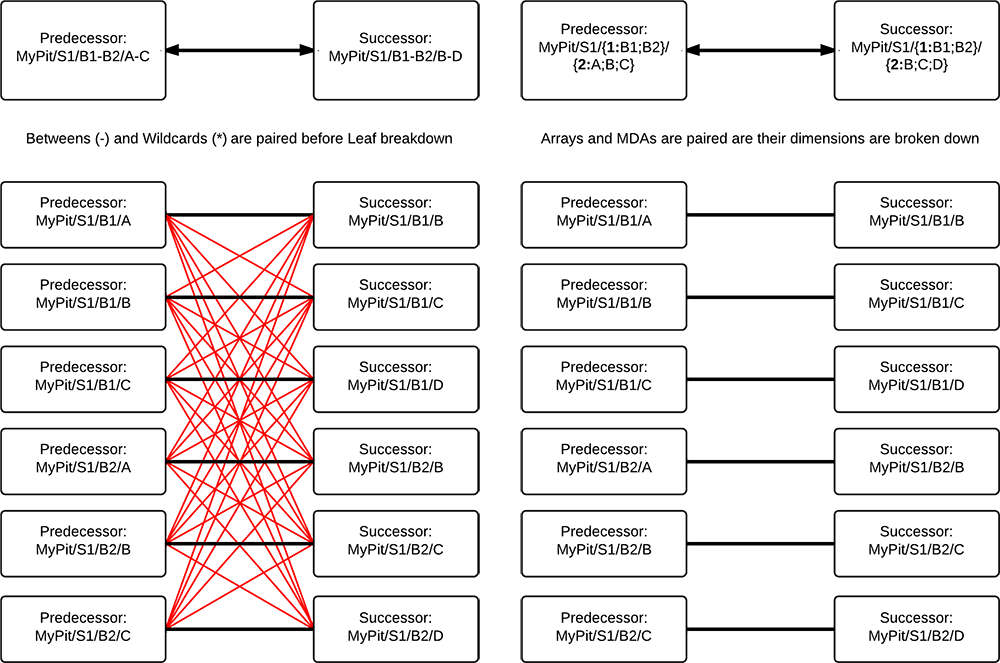
It doesn't really matter what number you give each array, as long as each array pair has the same length. Predecessor Array {1:} needs to match Successor Array {1:} in length and so on.

@Position, ..ArraySpan and #Jump (Range Dependencies)

Because of the pairing above, explicitly pairing items in Arrays is an important concept and the following tools will assist in pairing your predecessor and successors.

  • @Position: Uses the Index (rather than the Name) of a Position. @0 indicates the first item (zero indexed) and @-1 indicates the last (@-2 second last etc)
  • ..ArraySpan: Use this option instead of individual semi-colin delimited objects to Span multiple Positions. E.g. */*/*/*/{D..G} is the same as */*/*/*/D;E;F;G
  • #Jump: Use this option in conjunction with an ArraySpan to Jump more than one position at a time. E.g. */*/*/*/{D..G#2} is the same as */*/*/*/D;F

Example: The earlier array

Predecessor: MyPit/S1/B1-B10/{A;B;C;D;E;F}

Can now be written as

Predecessor: MyPit/S1/B1-B10/{@0..@-1}

Sequence Dependencies

Grouping Expression are relevant for Sequence (essential) and Solid Overlap (for performance) Dependencies. Also used in Table Plots and Proximity Contraints.

As the name suggests a Grouping Expression creates groups out of various Leaves in your Table. Dependencies are then created INSIDE each Group between the included Tasks (but not BETWEEN Groups). When considering what to include in a Grouping Expression you should think about what attributes are shared and include them in your expression. Conversely, you want to exclude attributes that you want to create interactions between.

For example in a "Dig Top Down" Dependency you want to create a Grouping Expression that includes your horizontal attributes (and excludes your vertical attributes). The resulting Grouping Expression would be similar to

Text(SourcePit) + "//" + Text(SourceStrip) + "//" + Text(SourceBlock)

Each Group created by this expression would share a Pit, Strip and Block but allow interactions between any other Levels, Positions and Tasks.

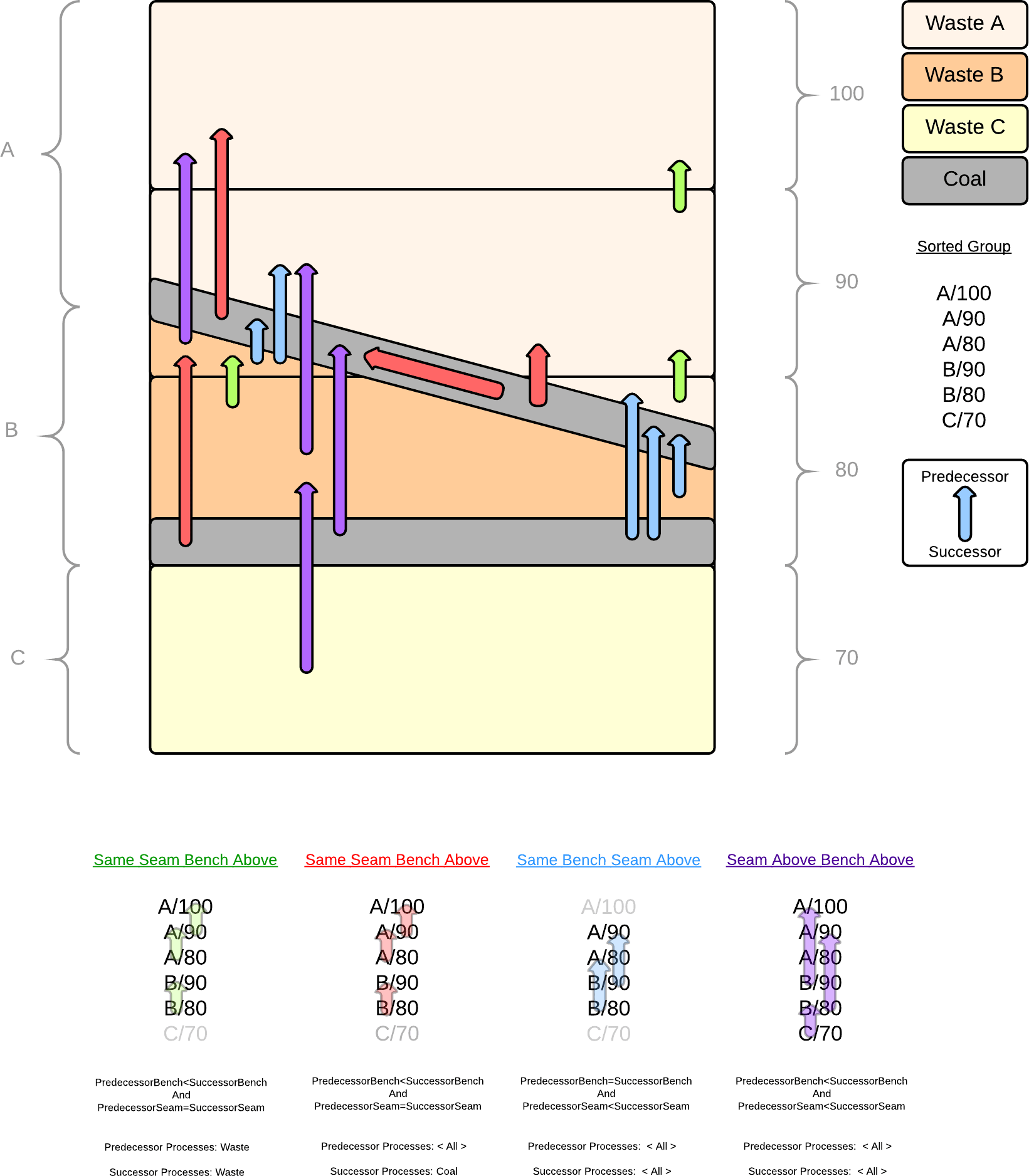
Leaf Lists

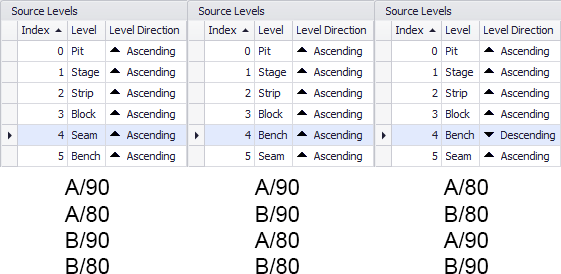
For each group created above, a list of Leaves are created. The order in which those Leaves are sorted relates to the Source/Destination Levels interface (The Index and Level Direction of each). If there are 4 Leaves in a group (A/90,A/80,B/90 and B/80) then these can be sorted in up to eight unique ways (three are below):

Dependency Entry Filters

By default, a Sequence Dependency only includes one Dependency Entry with a blank filter. Continuing the example above, what this does is creates a Dependency between sequential Leaves in the List (higher = predecessor, lower = successor). Using the first column this means 3 dependencies:

1: Predecessor: A/90 <All Processes> Successor: A/80 <All Processes>
2: Predecessor: A/80 <All Processes> Successor: B/90 <All Processes>
3. Predecessor: B/90 <All Processes> Successor: B/80 <All Processes>

This may be sufficient to create the type of Dependency you require but you may find you need a finer grain of detail than this. By filtering the Leaf List you can create multiple dependency entry in each group, so the following diagram demonstrates how to create a more robust top down Dependency.