Расчет траектории

Каждую пару последовательных точек съемки можно связать сегментом окружности. Касательная к окружности в каждой точке съемки - это вектор, образованный азимутом и наклоном в данной точке.

При использовании коротких дуг (арок) этих окружностей, ряд таких дуг сформирует траекторию скважины. При этом арки "округляются" до прямых линейных сегментов, расстояние между прямой и аркой никогда не превышает 0,05 метров.

Подробно

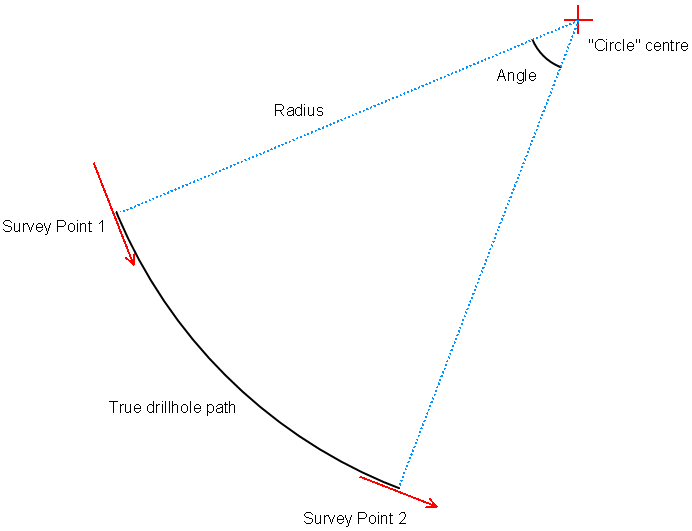
Возьмем две последовательные точки съемки. Положение первой известно (это может быть устье или рассчитанная конечная точка предыдущего сегмента). Используя азимут и наклон, построим два вектора, отображающие направление точек, а затем рассчитаем угол между двумя векторами направления.

На окружности угол между касательными в двух точках равен углу между двумя точками (если представить, что точки находятся на окружности). Радиус окружности можно рассчитать делением длины арки между двумя точками на угол между ними. Соответственно, нам известны: угол, расстояние между двумя точками (интервал). На основании этих данных мы можем рассчитать радиус круга.

Мы можем построить вектор, представляющий собой радиус:

временныйВектор = направлениеВектор1 x направлениеВектор2

РадиусВектор = направлениеВектор1 x временныйВектор

Затем мы можем использовать полученный радиус и известное положение первой точки для поиска центра круга.

центрКруга = начальнаяТочка - радиус * радиусВектор

Если радиус больше, чем двойное максимальное отклонение (около 0,05 м), то для сглаживания арки необходимы дополнительные промежуточные точки. Если угол между двумя точками больше, чем

уголШагРазмер =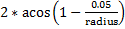

то количество сегментов линий, которое необходимо создать:

количествоШагов = (угол / уголШагРазмер)

Теперь мы можем использовать рассчитанные значения для создания линейного сегмента и точек, применяя поворот векторов. Для каждой точки:

новыйРадиусВектор = поворот радиусВектор вокруг временныйВектор по уголШагРазер * номер точки

сегментТочка = центрКруга + радиус * новыйРадиусВектор

Таким образом рассчитываются точки сегментов.