Трёхпараметрическое логнормальное

Трехпараметрическая логнормальная оценка активна только в просмотре графика, если масштаб во вкладке Данные ввода диалогового окна Масштаб настроен на НАТУРАЛЬНЫЙ ЛОГАРИФМ (Ln).

Нажмите кнопку Трёхпараметрическое логнормальное в панели инструментов графика, чтобы создать аддитивную постоянную, которая уберет выпады от логнормальных проб.

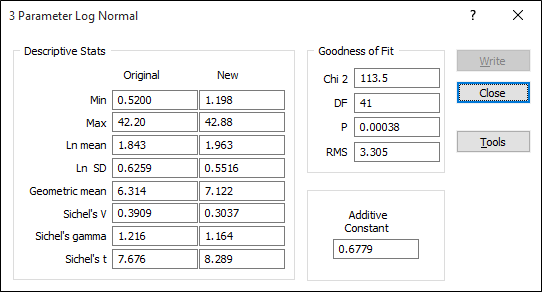
Аддитивная постоянная

Аддитивная постоянная - это число, необходимое, чтобы нормализовать (логарифмически нормализовать) набор данных. После запуска процесса вычисления, аддитивная постоянная отображается вместе с рядом измерений того, насколько точно измененные данные соответствуют логнормальному распределению, включая хи-квадрат, степень свободы, p-значение и среднеквадратичное значение.

После того как будет выбрана опция 3-параметрическое, на экране появится информационное окно, в это время функция будет обрабатывать данные. После того как вычисления будут произведены, появится другое информационное окно с заголовком 3-параметрическое Ln, смоделированные данные будут отображены на графике. В информационном окне Трехпараметрическое Ln отобразится таблица с колонками для исходных и новых значений: Минимальное значение, Максимальное значение, Ln среднее, Ln стандартное отклонение, Геометрическое среднее, Оценочная функция Сишеля, Дисперсия Сишеля и Гамма Сишеля.

Описательная статистика

Минимальное значение	Наименьшее значение, используемое в графике
Максимальное значение	Наивысшее значение, используемое в графике
Ln среднее	Ln среднее - это среднее логнормальных значений в графике. Геологические данные часто имеют логнормальное распределение Смотрите: Ln среднее
Ln стандартное отклонение	Логарифмическое стандартное отклонение является аналогом стандартного отклонения, это измерение распределённости данных. Его получают также, как и Ln среднее Смотрите: Ln стандартное отклонение
Геометрическое среднее	Геометрическое среднее - значение медианы логнормальной популяции. Как и для медианы для нормальной популяции, геометрическое среднее будет то же самое, что Ln среднее, если данные распределены логнормально. Смотрите: Геометрическое среднее
Оценочная функция Сишеля (t), дисперсия Сишеля (V) и Гамма Сишеля	t Сишеля - оценочная функция Сишеля - это альтернативное измерение среднего логнормально распределенных данных. Оно рассчитывается с использованием теории вероятности и корректирует ошибки в Ln среднем, если количество проб небольшое. Смотрите: Оценочная функция Сишеля

Качество подгонки

Тест Хи-квадрат (chi 2)	Хи-квадрат - это статистический тест, который измеряет "качество подгонки" данным. То есть измеряет, подходит ли набор измеряемых данных (проб) к выбранному виду распределения. Распределение, к которому подбираются данные, может быть как нормальным, так и логнормальным.
Степени свободы (DF)	Степени свободы могут быть заданы как количество наблюдений в пробах минус количество измеренных параметров из проб (Davies 1974). Эти определения на практике означают, что каждый раз, когда параметр, такой как среднее по пробам или данным, используется в вычислении другого значения (например стандартного отклонения), количество степеней свободы уменьшается на 1.
P	Значение Р (Значение Р) - это измерение вероятности, которое рассчитается при проверке на ошибки.
Среднеквадратичное значение (RMS)	Значение RMS (Среднеквадратичное значение (RMS)) является мерой “качества подгонки”. Значение является "интуитивным" измерением - чем меньше среднеквадратичное значение, тем лучше можно считать качество подгонки между распределением данных опробования и тестовым распределением.

Записать

Нажмите на кнопку Записать, чтобы записать исходные данные (в пробах) плюс аддитивную постоянную в переменную, заданную в диалоговом окне Гистограмма во вкладке Анализ в поле вывода 3-параметрическое Ln. Смотрите: Трехпараметрический логарифм

Алгоритм, на основании которого обрабатываются значения меньше минимального для графика и значения выше максимального для графика, определяется путем активации опции, связанной с добавочной постоянной для 3-параметрического Ln.