Хи-квадрат

Хи-квадрат - статистический тест, который измеряет "качество подгонки" данных. То есть с его помощью проверяется, подходит ли набор измеряемых данных (проб) к выбранному виду распределения. В зависимости от используемой вами функции Micromine, пробу можно сопоставить с Однородным, Нормальным, Логнормальным или Экспоненциальным распределением, настроив опцию Масштаб или Распределение соответствующим образом.

Тест Хи-квадрат делит набор данных на бины с фиксированной длиной. Бины, содержащие меньше пяти проб, объединяются с примыкающими бинами для получения более точного расчета, обычно это происходит в хвостах распределения данных опробования.

Для каждого бина рассчитывается ожидаемое число измерений и затем вычитается из подсчитанного числа измерений в этом бине. Чтобы это число всегда было положительным, результат возводится в квадрат и делится на число ожидаемых измерений. В конце результаты для бинов суммируются, чтобы создать статистику по критерию Хи-квадрат. Для того чтобы определить, соответствуют ли данные опробования распределению теста, это число впоследствии можно проверить в отношении критической величины. Критические величины для различных комбинаций степеней свободы и уровня значимости можно получить из стандартных статистических таблиц Хи-квадрата.

Если рассчитанное значение статистики критерия Хи-квадрат меньше, чем критическая величина, вы признаете, что проба соответствует распределению относительно которого она была протестирована. Вы можете прийти к такому же заключению, если р-значение будет больше уровня значимости.

В ином случае, если рассчитанная статистика критерия Хи-квадрат превышает критическую величину, либо если р-значение меньше уровня значимости, вы отклоняете распределение.

Уровень значимости представляет собой оценку того, насколько маловероятно вы будете допускать то или иное значение перед тем, как отклонить распределение. Несмотря на то, что уровень значимости может варьироваться от 0 до 100%, стандартными значениями будут являться 1%, 5% или 10%, где более высокие значения представляют более строгие статистические критерии.

Р-значение - это вероятность, связанная с критической величиной для данной степени свободы. Это проверка в отношении сходимости данных опробования с распределением, если р-значение становится меньше, вероятность того, что данные опробования будут соответствовать распределению, уменьшается.

Степени свободы (DF) - данный критерий равен количеству бинов минус 1. Он корректируется каждый раз при объединении бинов, это может привести к меньшему, чем ожидается, значению DF.

При проверке геологических данных в отношении нормального распределения, вы можете обнаружить, что часто отклоняете распределение. Однако, если распределение опробования имеет один пик и является приблизительно симметричным, тогда предположение о нормальности обычно дает приемлемые результаты (Wellmer, 1998, p.40). Данную концепцию можно расширить до результатов разбиения: если значение Хи-квадрата является относительно низким, а сходимость (подгонка) данных и модели выглядит верной, при совпадении пиков и минимумов, вы можете расценивать это разбиение как подходящее.

Значение Хи квадрат 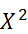задается как: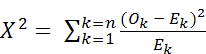

Где 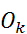- количество измерений в бине К,

а 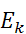- это ожидаемое число измерений в бине К

Ссылка: Wellmer, F-W., 1998. Statistical Evaluations in Exploration for Mineral Deposits. Springer-Verlag, Berlin. 379pp