Overview
By setting up at an unknown point, and measuring the horizontal angles between three points with known coordinates, it is possible to calculate the coordinates of the unknown point. This process is known as resection. If vertical angles to the known stations are also measured, then the Z of the unknown point can be calculated.
In the diagram below, U is the unknown point and P, Q, R and S are known points. If 3 known points (say P, Q and R) are used then there is a unique solution for U.
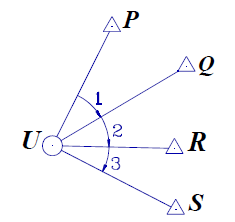
If more than 3 points are observed, then and there will be redundancy and an adjustment is required as part of the calculation.
The most rigorous solution requires a least squares adjustment. An alternate method is to calculate multiple unique solutions and to average the results.
In the above example the coordinates of U would be calculated three times, using the observations to PQR then PQS and finally QRS.
Although it is the angles between the fixed points that are used in the resection calculation, the field measurements are horizontal readings (directions) to the fixed stations. It is normal to take readings using both face left and face right (changing from FL to FR is achieved by rotating the telescope about its vertical axis by 180 degrees).

To further improve the measurement process several "rounds" of angles may be observed (a round is a set of face left and face right observations to all targets).
Generally, the horizontal circle of the theodolite will be shifted for each round. This means that the value of the horizontal reading to each target will be different for each round.